刘海涛

　　提到分形，可能有些人会感到很陌生。这是个什么概念，还是个什么东西？如果用最浅显但同时又貌似深奥的话来讲，分形就是“不规则的规则”。 

　　不规则的规则？这又是什么？ 

　　为了解释不规则的规则，我们先来看一下“规则的规则”：在经典的欧氏几何中，我们可以用直线、圆锥、球等这一类规则的形状去描述如墙、车轮、道路、建筑物等人造物体，因为这些物体就是按欧氏几何的规则图形生成的。目前，几何学里所研究的对象，大体上就是这样“规则的规则”的。但是，自然界中，却存在很多“不规则”的复杂的几何对象，如山脉、云烟、波浪、树木、闪电，以及星团、短痕、浸润、冲积扇、泥裂、冻豆腐、水系、晶簇、蜂窝石、小麦须根系、树冠、支气管、星 系、材料断口、小肠绒毛、大脑皮层……等，它们无法用经典几何图形来描述，人们发现，没有传统的数学模型可以对它们进行研究，因为它们不再具有我们所早已熟知的连续、光滑可微这一基本性质了。这一大类形状奇怪的图形长期以来被认为是“不可名状的”、“病态的”而很容易被人们忽视了。 

　　那么这种不规则怎么还能称之为“规则”呢？请看下图的例子： 

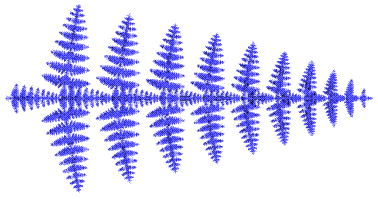
　　这是一片叶子，那请问它规则吗？我们从第一感觉上来说，它貌似很美，很规则（因为大家往往把规则的东西看成美，所以美的东西往往就显得规则了）。但是，这片叶子却不是可以像车轮，楼房一样用经典的欧氏几何中的一些规则形状就能描述的。试想，我们能用直尺和圆规画出图中的叶子吗？ 

　　也许有人说能。是的，是可以的；但是，那将是一个漫长的工作。而且，在画图的过程中，我们就已经运用了分形的概念，虽然表面上我们只是用直尺和圆规，但我们却在不自觉地运用着“分形”，也就是“不规则的规则”。为什么这么说？我们再看一个经典的分形例子，Koch雪花： 

　　我们取一个边长为1的正三角形，第一步，将每边三等分，以各边的中段为边，向外作小的正三角形，并去掉原来的中段，得到一个星形十二边形；第二步，继续将此十二边形的每条边三等分，以各边中段为边向外作更小的正三角形并去掉原来的各个中段，生成一个48边形；如此继续下去以至无穷，得到的极限曲线是连续的但在任何地方都没有确定的切线，如上图所示。 

　　如果对比叶子的图片，我们是不是会感觉到这两幅图有什么相似之处呢？ 

　　是的，它们在某种程度上很相似：都是不规则的，但都蕴含着规则之美。这可以用分形的定义来说明：分形集是一类不能用经典几何方法描述的“不规则”集合，它们基本满足分形的经典性质，但是在自相似的程度上可以有很大差别。而什么又是分形的经典性质呢？从几何学上看，分形是实空间或复空间上一些复杂的点的集合，它们构成一个紧子集，并且具有下面经典的几何性质：分形集都具有任意小尺度下的比例细节，即具有无限精细结构；分形集无法用传统几何语言来描述，它不是某些简单方程的解集，也不是满足某些条件的点的轨迹；分形集具有某种自相似形式，包括近似和统计上的自相似；分形集一般可以用简单的方法定义和产生，如迭代；按某种维数定义，分形集的分形维数大于相应的拓扑维数。 

　　概念性的东西总是很难理解，但我们将这个概念与Koch雪花联系起来，相信会豁然开朗许多。这就是分形，不规则中的规则。我们知道材料中有一类结构叫做“准晶”，那么，这种不规则的规则是不是就可以叫做“准规则”了呢？ 

　　将Koch雪花应用到现实的一个例子是海岸线模型：到过海边的人都见过海岸线，我们也常常见到介绍某国的文字中有“某某国有海岸线多长多长”的字样，那么，这个数字准确吗？它是怎么算出来的？分形概念的提出者数学教授Mandelbrot于1967年在《Science》杂志上发表了一篇富有启发性的文章，题目就叫“英国的海岸线有多长？”（How long is the coast of Britain？）。文章中说，海岸线这种曲线的度量是无法得到一个确定的答案的，测定的长度依赖于所采用的测量的尺度。如果测量单位较大，就如同远距离观察的效果，较小的海湾是不可能看到的，所以在测量中无法得到反映。当你接近海岸线时，相当于以较小的度量单位作出测量，一些较小的海湾就变得清晰了。如果再缩小尺度，那么海湾的细节也可以观测到，尺度足够小时，海岸线的更精细的凹凸波动都可以清晰地显现出来，因此，Mandelbrot断言，海岸线的长度是不确定的。貌似这时，我们似乎又可以说分形还是一种“规则的不规则”了。 

　　这就是神秘而熟悉的分形。