邱锐浩

准晶体，是一种介于晶体和非晶体之间的固体。准晶体具有与晶体相似的长程有序的原子排列，但是准晶体不具备晶体的平移对称性。它像是一种阿拉伯式的原子镶嵌图，华丽，迷人而又充满神秘的异域风情。

1982年，以色列科学家谢赫特曼用电子显微镜测定了他自己合成的一块铝锰合金的衍射图像，发现是一个正十边形的对称结构——对寻常晶体来说这是一个不可能的对称性，因为从数学上很容易证明你不可能用正十边形（或者简化到正五边形）去周期性地铺满平面。谢赫特曼认为这是一种全新的晶体，它的特点就是只具有准周期性，也就是“准晶”。Ilan Blech 帮谢赫特曼搞出了一个数学模型，二人这才决定发表论文，结果被APL编辑拒稿。接下来谢赫特曼回到国家标准局，在John Cahn帮助下进一步完善了数学，然后找到一位真正的晶体学家Denis Gratias入伙，最后文章被PRL发表。

图1.

但是当时只有少数科学家接受这是一种新晶体。关键在于，谢赫特曼实验使用的是电子显微镜，而晶体学界的标准实验工具是更为精确的X射线，他们不太信任电子显微镜的结果。不能用X射线的原因是生长出来的晶体太小。一直到1987年终于有人生长出来足够大的准晶体，用X射线拍摄了更好的图像，科学家中的“主流”才接受了准晶的发现。

经典晶体学中，无论是14种布拉菲点阵还是230种空间群，均不不允许有五次对称，因为五次对称会破坏空间点阵的平移对称性，即不可能用五边形布满二维平面，也不可能用二十面体填满三维空间。而准晶的发现颠覆了这种观念，准晶的特点之一就是五次对称性。其实，矿石界的蛋白石，有机化学中的硼环化合物，生物学中的病毒，都显示出五次对称特征，而数学家们早已为准晶做好了理论铺垫，1974年，英国人彭罗斯（Roger Penrose）便在前人工作基础上提出了一种以两种四边形的拼图铺满平面的解决方案，如图2。对于Shechtman的准晶体衍射图案和彭罗斯的拼图来说，都有一个迷人的性质，就是在它们的形态中隐藏着美妙的数学常数τ，亦即黄金分割数1.618……。彭罗斯拼图以一胖一瘦两种四边形（内角分别为72度、108度和36度、144度）镶拼而成，两种四边形的数量之比正好是τ；同样的，在准晶中，原子之间的距离之比也往往趋近于这个值。接着，1981-1982年，Mackay把Penrose的概念推广到三维空间，两种三十面体穿插起来得到的二十面体对称性，并用光学变换仪得出五次对称的光学衍射图。

图2

众所周知，五次对称性和周期性是不能共存的。如果坚持五次对称，就必须考虑准周期性。如图3，沿与5次轴正交的一个轴看去（用箭头表明），线段的长度并不是随意的，而仅有一长一短两种，他们的比值恰好是黄金分割数1.618…，且图中所有夹角都是/5的整数倍。也就是说，虽然这种二维结构中不具有周期性，但也不是完全混乱无序的，无论是长度还是夹角都有定值。

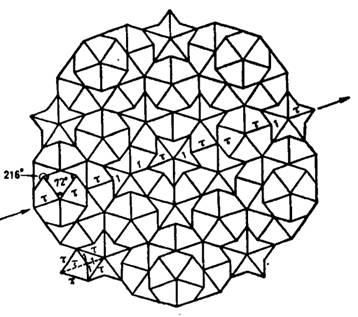
图3

准周期性的特征是无理数，在一维准周期点阵中，除了平移单位1外，还可平移。图4（a）中是一个二维正方点阵，选取斜率为的条带，将其上的点投影到一维空间E//（水平空间）中，构成长度分别为L和S的一维准周期点阵，LSLLSLSL……。这个一维准周期点阵的特点是S两旁无S近邻，L两边最多只有一个L近邻。由于条带斜率是无理数，其边线只能通过一个阵点，若其斜率改为有理数2/1，如图4（b），则条带在平行空间中的投影变成周期性的LLSLLS……。由此可知，一维周期的点阵和一维准周期点阵都可以由一个二维周期点阵投影获得，所不同的仅仅是选取的投影带的斜率，前者是有理数，后者是无理数。

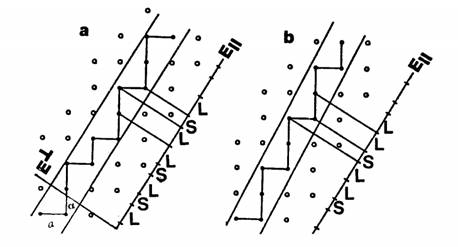
图4

有趣的是由于光的丰富的色彩与准晶体独特的几何结构相结合，将表现出非凡的艺术性。在许多领域的研究中所呈现的准晶图样如准晶聚合物结构，准晶的衍射图样，光子准晶中谐振状态的分布强度等都有很高的艺术欣赏价值。

西班牙Alhambra宫和伊朗Darb-iImam清真寺里的非周期性镶嵌图样正反映了准晶图样与建筑艺术的完美结合。

日本艺术家Akio Hizume从准晶中获取灵感，用510根小竹杆创作出三维准晶作品。

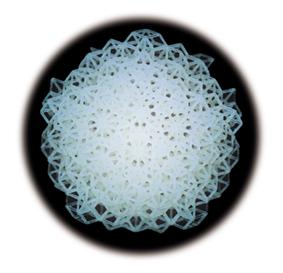
准晶聚合物（quasicrystalline polymer）结构

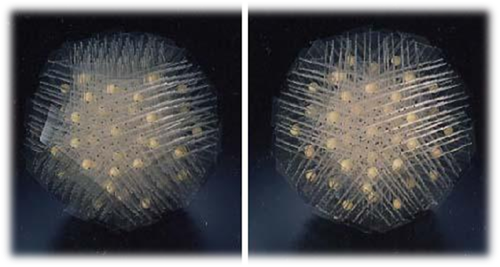
准晶衍射图样

光子准晶中谐振状态的分布强度，红色对应高强度，蓝色对应低强度

西班牙Alhambra宫和伊朗Darb-iImam清真寺里的非周期性镶嵌图样

日本艺术家Akio Hizume利用小木杆做出来的准晶模型

（注：图片来自网络）